Sorry Guys

Well, since it's summer and almost nobody is in school, I have decided that all posting on this blog will come to a halt until the end of August, beginning of September. I am sorry for all of you dedicated followers whom rely on me for assistance.

~dem0nd~

Domain and Range

         Two of the most reoccurring words in high-school math are Domain and Range. Honestly, it is a lot easier to figure these out than most math teachers let on. Putting it plain and simple, the 'Domain' is the 'x' term in a coordinate pair, and 'Range' is the 'y' term.

As an example:

(2,4)(3,3)(1,9)(8,7)

In the coordinate pairs above the domains and ranges are as follows:

Domain: (1, 2, 3, 8)
Range: (3, 4, 7, 9)

It is literally that easy!
Any questions? Comment!

Multiplication in Your Head: 2 Digits

Have you ever wanted to be able to do 2 digit multiplication in your head without a calculator? Well here is a quick and easy way:

24*16=?

20*10 = 200
20*6   = 120
10*4   =   40
6*4     =   24
               384

See how easy that is? Now you can blast through those multiplication problems!

Google Mathway

Today I stumbled upon a grand new tool. It is called Google Mathway, and can be found here. This is much like a super-calculator and can be used to solve thousands of problems from basic addition all the way to Differential Equations. This could be a very valuable tool and I highly suggest giving it a shot! There is even an option where you can see exactly how it solved the problem.

Technicalities of Lines, Rays, and Line Segments

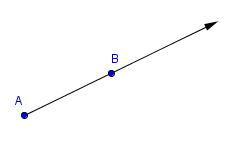
Some algebra and geometry teachers can be real sticklers when it comes to these three models. There are slight differences between the three and I'm going to help you separate them.

A Line Segment  has two define endpoints, which is how it is labeled, and has no arrows as follows:

Line segment AB:



A Line is like a line segment, in which it is identified by two points. The line however continues on in both directions, so the ends are marked with arrows:

Line AB and Line GH:


A Ray is a nice healthy mix of the two. One end ends in a point, while the other has an arrow. A Ray also is identified by two points:

Ray AB:


Any Questions? Please, comment. I am more than willing to help you with anything you need. :)

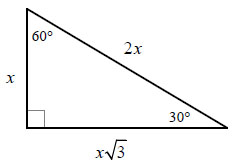
Special Right Triangles: 30-60-90

Special Right Triangles again? you might ask. Indeed there is more. This type of Special Right Triangle is called the 30-60-90. This is because it contains one 30 degree angle, one 60 degree angle, and one 90 degree angle. Solving these is fairly similar to the 45-45-90 triangles. Here is an example:

The short leg, 'x', is always opposite the 30 degree angle. The hypotenuse, is always exactly 2 * 'x', and it will always be opposite the 90 degree angle. And lastly, we have the long leg, always opposite 60, and is 'x' times the square root of 3.

In this example, we are going to solve for 'x' and 'y'.

First, we are going to solve for the short leg which in this case, is 'x'.

Since we know that 4 square roots 3 = 'x' square root of three,  we know that 'x' is equal to 4. This is because to get 'x' by itself, we need to divide both sides by the square root of 3. The equation would then be set to x = 4.

Now, to solve for 'y' all we have to do is double the short leg. Since we now know the short leg is 4, we know that y = 8.

And that is all you have to do to solve 30-60-90 triangles!! 

As always, if you are even a little bit confused, comment!

Disclaimer

There may be advertisements on this blog in the future in order to generate income. Sorry if this is an inconvenience.

Random

Why does the fire stay a simple diameter?

Special Right Triangles: 45-45-90

Hopefully we all know what a right triangle is. A right triangle is a triangle that has one 90 degree angle within it. Special right triangles come in two varieties.

First off, there is the 45-45-90 triangle. As the name suggests, it contains one right angle, and two 45 degree angles.

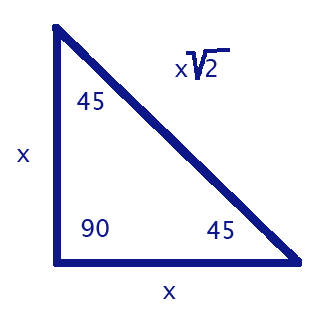This is fairly basic. The two legs, (the two sides that are touching the 90 degree angle) are both 'x' because they are congruent. The hypotenuse is simply x square-roots of 2. If the length of each leg was, lets say 5, x would equal 5. The hypotenuse would then be  square roots of 2. Really, for a problem like this, you don't even need to do the work. You just need to know that if the problem  gives you the length of a leg, then the hypotenuse is that number, times the square-root of 2.

Another way they will give you this problem is they will give you the hypotenuse and you have to solve for the legs.

Here, what we would do, is set up an equation. This might end up looking weird for there is no character for the radical.

       1.25=x (square root 2)
We do this because as shown in the first diagram, the hypotenuse is equal to x times the square root of 2. Now we want to get 'x' by itself. So we divide both sides by the square root of 2.

              1.25         = x
       square root 2

The general rule of thumb when dealing with radicals (square root signs), is that the cannot be in the denominator, or the bottom of the fraction. To get rid of it, we are going to multiply both the top of the fraction and the bottom by the square root of 2.

              1.25 * square root of 2     = x
                           2

Square root of 2 times the square root of 2 is 2. If the first numerator, in this case 1.25 was even, then you could simplify further, but for this problem, we aren't going to have to.

As always, if you have any questions, comment!

Geometric Mean

Something that plagues many geometry students is geometric mean. To be perfectly honest, there are few real life applications for this, but here we go:

Geometric Mean of Two Numbers:
If a question states something such as:

       Find the geometric mean of 75 and 10.

This is how you would write it out:

 x  = 10 
75     x

To solve, you would first cross multiply, or multiply diagonally.

x² = 750

Did you follow?
Now we are going to do the square root of both sides in order to get 'x' by itself:

x = 27.4 (Rounded to tenth)

If I was confusing, which I often am, comment, and I will attempt to clarify!

Khan Academy

One of the most efficient ways to understand math is to head on over to Khan Academy. They area great learning resource for students of all levels. Make sure to check it out!